If you still want to follow me, please update your subscriptions. The new blog you can follow by Facebook/Twitter or RSS.
The new address is: https://piotr.westfalewicz.com/blog/
[__DynamicallyInvokable]
Patterns C# Software Information Architecture Design Technology Big .NET Data Microsoft Development
Friday, November 3, 2017
Thursday, October 12, 2017
Rock solid pipeline - how to deploy to production comfortably?
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2017/10/rock-solid-pipeline---how-to-deploy-to-production-comfortably/
First of all, this post won’t be for people who think developer’s job is to design, write code and test it. It’s far beyond that. One of the important responsibilities is to ship your code to production. How to do that safely?
Starting with the artifacts
Where do we begin? Assume you designed, wrote the code, tested it, reviewed it, wrote integration tests, added logging, metrics, created documentation, updated dependencies/libraries, pushed the code to some kind of a repository (doesn’t matter which one) and your build system created runnable version of your code with the all needed content – you have the ARTIFACTS for the deployments. So now what?
For deployment and code validation purposes we use a pipeline. It’s a series of verification steps which ensure our code is working as required. How many stages should the pipeline have? What stages should it have?
 |
| A pipeline. Edit it on draw.io. |
Understanding the tradeoffs
Of course, it will depend on your use case. You have to find the balance between time to production, time invested in the pipeline (tests, monitoring, infrastructure…) and validation strictness. StackOverflow stated on one of their presentations that they test the software on their users. While it may work for them, imagine a bank testing the software on the end users. In some cases, the trust is too important to lose. This post will present rock solid pipeline for one development environment and multi-region production environment. If executed correctly, it’s a pipeline which will catch nasty things like memory leakage or minimize blast radius in production.Rock solid pipeline
 |
| Rock solid pipeline. Edit it on draw.io. |
The orange cards are validation steps. Once all requirements in validation steps are completed, the change is promoted to the next environment.
The environments
- The artifacts – not really an environment… but the graph looks nice with it :)
- Alpha – environment only for tests purposes. It’s not facing any real traffic. The main purpose is to make the beta environment stable - to catch errors before they will reach development environment and cause cross-team failures.
- Beta – this is the development environment.
- Gamma – again, an environment which isn’t facing any real traffic. It’s very important though, because it is configured identically as the real production environment.
- 1 Box – a small subset of production hosts. Surprise! Not really 1 host… if your service runs on 1000 hosts, you can have, for e.g. 10 of 1 Box hosts.
- Production.
Validation steps
First of all, before deploying the changes anywhere, rudimentary checks can be done. Unit tests can be ran, static analysis can be performed – if code review by right people is done, if the change follows the code style, if the code is covered by unit tests. All checked? Proceed to Alpha.
After Alpha deployment, part of integration tests can be executed. It may be impossible to execute all of the integration tests and keep sensible execution time. Pick the most important ones. As previously written, Alpha is to keep the Beta (development env) stable. By integration tests, I mean all automated test which interact with the environment in any way. While executing the tests, scan the logs for ERRORs. The errors amount has to be kept in reasonable limits. Poorly written code will result in treating the presence of the errors as a normal situation. No issues discovered? Proceed to Beta.
Beta is the development environment. It’s the environment used for demos or manual testing. It’s used heavily through the company, so any issues here will cause time loss for many teams. The change will spend here quite some time and will get tested thoroughly. This is the time to run all integration tests and load tests. Load tests should aim at least production peak volume (scaled per number of hosts). During all this time when different tests are executed and people are using your service, monitor the logs as before. Validate if the logs are produced at all. Use different metrics:
- Host level (CPU usage, thread pool, memory, network IO, disk IO, disk usage, file handles/Inodes number).
- Application level, that is specific to your business, for example:
- Number of invalid sign-ups, average size of sent messages.
- Latency of the downstream APIs, number of requests to the downstream APIs, number of requests to your APIs, latency of your APIs, number of errors returned, number of exceptions thrown.
Monitor those metrics with different kinds of alarms. Most basic one: check if the value is between min/max values. However, there are more powerful and more sophisticated types: first derivative or σ value checks. More on those in the next post. Rigorous tested passed? Proceed to Gamma.
Gamma is a special environment, because it is the first environment with production configuration. The only validation is smoke integration tests, which uses different components of the service to check the configuration. The purpose of those tests is to catch, for example, mistyping in production connection string. Seems to be working? Go to 1-Box.
1-Box, as written previously, is part of your production fleet. It should be a small percentage of production hosts, serving production traffic. Despite obvious reduction of blast radius by number of hosts, there is an additional benefit in some situations. Taking as an example processing messages from a queue, if the faulty 1-Box will take the message and fail, there is a high chance that later on a healthy host will take the message and there will be no customer impact at all. To further reduce blast radius, deploy to one 1-Box region at one time, obviously at off-peak time. After deployment is made, monitor what was monitored in Beta (logs, hosts metrics, application metrics), however now you are performing validation against real production traffic. What’s more, here you can add one more peculiar type of check - compare the Production metrics to 1-Box metrics. This should hopefully reveal any anomaly missed before. After that, go for Production!
Finally, after ~2 days your change arrives in production. We are not perfect, what if critical bug is introduced! Does that mean we have to wait 2 days for a fix? Nope – deploy hotfix as you wish. You can for example skip the two “baking” processes and leave other validation steps in place.
Please note: the views I express are mine alone and they do not necessarily reflect the views of Amazon.com.
Wednesday, July 5, 2017
The nightmare of large distributed systems
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2017/07/the-nightmare-of-large-distributed-systems/
There are certain classes of exciting problems which are surfaced only in a massively distributed systems. This post will be about one of them. It's rare, it's real and if it happens, it will take your system down. The root cause, however, is easy to overlook.
Assumptions
For this post sake, let's make some assumptions:- Critical service is a service which is crucial from your business perspective, if it goes down, you don't make money, and your customers are furious.
- Your business is a veterinary clinic - or rather - immense, world-wide, distributed, most popular, top-notch veterinary clinic network. You make the money when the clients sign up online for visits. A critical service would be any service, which prevents the client from signing up. Let's call the path of signing up a critical path.
- The massive distributed system is a system consisting of, for example, 333 critical services, each one of them has it's own fleet of 1222 hosts (so in total, there are 406926 hosts running critical services in your system).
- Each critical service is managed by a two pizza team.
All in all, I'm thinking about something like this:
 |
| Large distributed system - exponential failure problem |
We have a customer, who want's to sign up, the load balancer takes the request, there are 332 healthy services involved, and there is this one red-star service, which is asked 4 times on the critical path. If it goes down, the customer can't sign up. I would compare it to kind of SELECT N+1 problem.
In such a big system, it may happen that a particular, red service will be called 10+ times on a single sign up. The sign up itself may have many steps, and each step may call many services, including our red service, many times. Architecture smell... design smell, you may tell... Yes and no. Think about the scale. 333 critical services, times two pizza teams = around 1333 people involved in just the critical path. Many more involved for non-critical services. I think this situation is inevitable at scale.
Problems
Availability
When the red service is down - that's an obvious situation, easy to spot. What happens if our service has some kind of issues that leads to 90% availability? What is the customer impact, assuming 10 calls made to the red service during sign up? Unfortunately, only 35% of customers will be able to go through the critical path. Why? The first call has 90% chances of success, the second call has also 90% chances of success, but both calls combined have only 0.9*0.9 chances of success. For 10 calls, that will be 0.9^10= ~35%. Unfortunately, in case of "system is down" event, while having enormous amount of alarms going off, tens of services impacted, loosing many customers each second, 10% drop in availability in one service is very, very easy to miss.
Timeouts
The second nasty problem is with the timeouts. The origin of the timeouts can span network problems, hosts problems, code bugs and more. It may happen that random 10% of requests will time out. Let's assume the red service has normally 20ms latency (on average). It's being called 10 times, so total wait time on a single sign up is 200ms. However, with those 10% timeouts, let's say 1.5 seconds each, changes the average latency to 20ms * 0.9 + 1500ms * 0.1 = 168ms. Now the total wait time for the red service is 1680ms. Probably the customer is getting timeouts at this point. It's nasty, because the 10% timeouts issue can be well hidden. For example, it might be a core router which is misbehaving, but still works and our monitoring doesn't discover the packet loss.
TL;DR;
Even tiny issues - like 10% timeouts or 10% availability drop - of only one service out of hundreds on a critical path in large distributed system can take it down.
Please note: the views I express are mine alone and they do not necessarily reflect the views of Amazon.com.
Please note: the views I express are mine alone and they do not necessarily reflect the views of Amazon.com.
Monday, June 5, 2017
What does it mean to design a highly scalable system?
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2017/06/what-does-it-mean-to-design-a-highly-scalable-system/
Please note: the views I express are mine alone and they do not necessarily reflect the views of Amazon.com.
It's surprising how the volume of data is changing around the world, in the Internet. Who would have thought 10 years ago, that in future a physical experiment will generate 25 petabytes (26 214 400 GB) of data, yearly? Yes, I'm looking at you, LHC. Times are changing, companies are changing. Everyone is designing for scale a tad different. And that's good, it's important to design for the right scale.
Over scaling
Let's assume you are a startup building a brand new, unique CMS (unlike the 2000 other ones). Is it worth thinking about NoSQL/Cassandra/DynamoDB/Azure Blob Storage? Probably not. It's safe to assume that most of data will fit into one small or medium SQL database. When performance problems will appear, that's good. It means your startup is working (or you just don't know SQL...). That means you have clients, paying clients. Also, at that point you will have probably completely different idea about the system - you gone from "no clients and your imagination only" state to - "working product with customers and proven solutions" state. You can reiterate over your architecture now. Hopefully you have founds now. What I've heard multiple times is failing a startup because someone created complicated, scalable system for 321 000 clients. All the money is spent on IT, none on business. Total failure.No need for scaling
Now, some systems don't have to scale, or the requirements with scale progress slower than the progress of the new hardware (so effectively they fall into the first category). Probably some ERP systems for most medium sized companies are good example. Large SQL database, maybe an Azure Blob Storage/DynamoDB and all scalability problems are solved.Some scaling needed
As I mentioned before, sometimes throwing an NoSQL database into the "ecosystem" solves the problem. Unfortunately for us, geeks, that's usually the case.Scaling definitively needed
There are times when people say "Azure Blob is highly scalable". Well, that statement is a joke. Azure Storage isn't scalable at all. Theirs 20 000 Requests Per Second limit sometimes might be a only a tiny part what you need. Furthermore, there are other, hard limits: Azure Storage Scalability and Performance Targets. To be fair, DynamoDB has limits too. However, you can contact support and request as much throughput as you need. There is one more catch too - pricing. In Azure you pay for requests amount (not throughput) + storage, in DynamoDB for provisioned throughput + storage. Depending on your use case, one might be much cheaper than the other.Unique scale
Finally, there are times when you need to build a new solution and even have a dedicated team for your challenge. Let's imagine you work at a big company, your company has hundreds of thousands of services, each service is called many thousands of times per second, and each call is generating logs. You want a solution to store the logs for months and search within them. The scale is unusual, and it's expected the number of calls will grow 30% year over year, having 4x more traffic on some days. This time, you can probably start thinking about your own, new storage engine, strictly coupled to your needs.TL;DR: covered some scalability levels, turns out everyone should scale different.
Thursday, February 23, 2017
Cassandra logs/time series storage design - optimal compaction strategy
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2017/02/cassandra-logs/time-series-storage-design---optimal-compaction-strategy/
 |
| Source: http://www.ccpixs.com/ |
Of course, all mentioned steps bring you closer to the success. It's good that there are plenty of great resources on how to design time series model in Cassandra. Just google "time series design Cassandra".
Surprisingly, the first five of them (dunno about others), don't mention setting the right compaction strategy.
The default compaction strategy (Size Tiered Compaction Strategy)
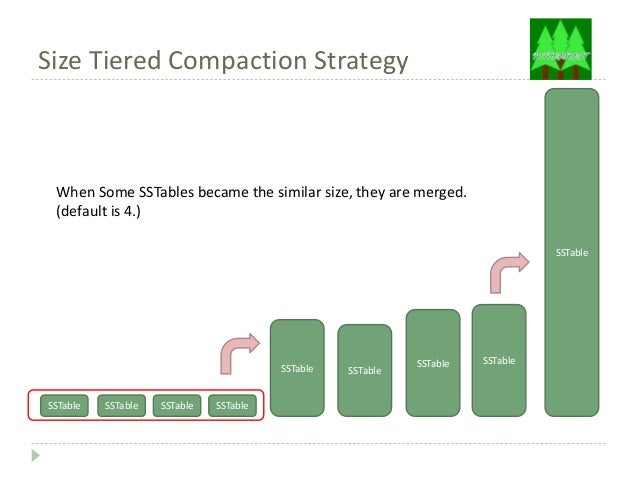 |
| Source: https://www.slideshare.net/tomitakazutaka/cassandra-compaction |
Solution: Date Tiered Compaction Strategy
 |
| Source: http://www.datastax.com/dev/blog/datetieredcompactionstrategy |
All in all, invoking this CQL (with carefully chosen consts), will save your cluster:
ALTER TABLE myprecouslogs.myprecioustable WITH compaction = { 'class' : 'DateTieredCompactionStrategy', 'base_time_seconds':'XXX', 'max_sstable_age_days':'YYY' }and here is how to do it on a live organism: How to change Cassandra compaction strategy on a production cluster.
BTW. Do you know that there is also anticompaction?
Tuesday, February 21, 2017
[Backup] Why shouldn't you ever use ResilioSync? "Database Error" problem
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2017/02/why-shouldnt-you-ever-use-resiliosync-database-error-problem/
As they say: there are two kinds of people in the World -those who pick up the ice cube that falls on the floor, and those who kick it under the fridgethose who back up their files and those who haven't experienced losing all their files yet.
Which category do you fall in?
I decided to set up a backup system with ResilioSync - the heir apparent of the BitTorrent Sync software. Well, that wasn't good idea and I don't recommend anyone using this software.
Maybe it's me, however I prefer the backup software to be:
- working and rock solid... dependable... stiff... hard... proven software
- well documented
- actively maintained (security patches, support)
Whereas my experience with ResilioSync turned out to be:
- Working... kind of. That was until I've updated it. I don't remember precisely from which version to which version and you won't guess that from dates too, because the releases doesn't have dates. I believe that was from 2.4.3 to 2.4.4. Maybe from 2.4.X to 2.4.X. I'm sure the major number didn't change. It's so important, because the ResilioSync showed "database error" after upgrading. Bummer. This problem alone, caused that I exterminated that piece of software from all my devices. No, I didn't wan't to check why it happened, because it shouldn't happen at all. When my primary data would be gone, I would have lost my data.
- The documentation is poor. You won't find it easy to follow. Sometimes you won't find what you are looking for at all.
- There is very limited amount of activity on ResilioSync official forum. You also can't help yourself looking at the code, because it's closed source. My question about HTTPS still has no answer after 5 months.
This, of course, is just my opinion.
Wednesday, December 21, 2016
Dynamic Programming and the hardest problem on HackerRank
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2016/12/dynamic-programming-and-the-hardest-problem-on-hackerrank/
The hardest problem on HackerRank, sorted by Max Score and level "Expert" is Separate The Chocolate. It's worth 250 points and the level "Expert" is the highest one. How to solve it?
Problem Statement
Tom and Derpina have a rectangular shaped chocolate bar with chocolates labeled T, D and U. They want to split the bar into exactly two pieces such that:
Input Format
- Tom's piece can not contain any chocolate labeled D and similarly, Derpina's piece can not contain any chocolate labeled T and U can be used by either of the two.
- All chocolates in each piece must be connected (two chocolates are connected if they share an edge), i.e. the chocolates should form one connected component
- The absolute difference between the number of chocolates in pieces should be at most K
- After dividing it into exactly two pieces, in any piece, there should not be 4 adjacent chocolates that form a square, i.e. there should not be a fragment like this:
XX
XX
The first line of the input contains 3 integers M, N and K separated by a single space.
M lines follow, each of which contains N characters. Each character is 'T','D' or 'U'.
Constraints
0≤ M, N ≤8
0≤ K ≤ M * N
Output Format
A single line containing the number of ways to divide the chocolate bar.
My approach
I didn't have any ideas how to solve it with DP. I've coded a solution which checks every possible way of chocolate division. I felt it wasn't the right solution because the complexity of that is exponential. The graph of possible permutations is checked wisely - at each "branch" I check the required conditions (connectivity, if K difference can be met, squares presence) and cancel the computation of subtrees with invalid state. The result? Quite nice: 16 out of 19 tests passed, 210.53 out of 250 points scored. I looked at the leaderboard, and noticed despite the winners many scored just like me. I've optimized some cases, however that wasn't enough. DP was indeed needed. I've tried to figure it out but finally gave up.
The solution
The whole editorial provided by HackerRank is very short:
This problem is a complicated dynamic programming problem (DP). The idea is simple but the implementation is difficult.We can iterate the grids one by one. For each grid suppose the left and the upper one has been given to Tom or Derpina. (Color black or white.)To decide the square [i][j], we need all the square’s state in square[i][0..j – 1] and square[i – 1][j..n -1] , all the (n + 1) squares in total can decide this square’s state. We can use these as a part of state and we also must keep whether a component is dead. (If it’s dead then add one more square of the same color is invalid.)
I can't wrap my head around the DP function though. It is strange for me that the vertical line will be the DP state - because the connectivity must be met for the whole matrix... anyone got an explanation?
Lessons learned
- If you can solve a part of a very hard problem - it still can be very profitable in terms of HackerRank score. Compare 210.53 points to 50 points from "Two Robots" medium problem.
- Looking at other's solutions, I've noticed this piece of code: Right after adding those three cases to my code, the result was 250 points (not counted towards HackerRank score, of course). Therefore: not everybody plays fair.
Thursday, November 24, 2016
Dynamic Programming in 5 easy steps - Examples - Two Robots
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2016/11/dynamic-programming-in-5-easy-steps---examples---two-robots/
This time we will solve a HackerRank problem, rated as a medium in difficulty. It's advised for you to go through a similar, but in my opinion easier problem described by me previously. The problem statement is as follows:
You have a warehouse with M containers filled with an infinite number of candies. The containers are arranged in a single row, equally spaced to be 1 meter apart. You also have 2 robots that can pick up 1 piece of candy and transport it between any two containers.Reminder - the 5 easy steps are:
The robots take instructions in the form of queries consisting of two integers, Ma and Mb, respectively. To execute a query, a robot travels to container Ma, picks up 1 candy, transports it to container Mb, and then stops at Mb until it receives another query.
Calculate the minimum total distance the robots must travel to execute N queries in order.
Note: You choose which robot executes each query.
- define subproblems, count number of subproblems
- guess (part of solution), count number of choices
- relate subproblem solutions, compute time per subproblem
- recurse + memoize OR build DP table bottom-up check subproblems acyclic/topological order, time = time per subproblem · number of subproblems
- solve original problem: = a subproblem OR by combining subproblem solutions ⇒ extra time
Step 2. Now, we basically have two choices, A: proceed with the first robot or B: with the second robot. When A - we add the distance of moving the r1 from it's last place Mb(r1) to Ma(INDEX), otherwise B: we add the distance of moving the r2 from it's last place Mb(r2) to Ma(INDEX). Additionally, in both cases we have to add the cost of moving Ma(INDEX) to Mb(INDEX).
Step 3. Writing the DP function is now straightforward:
DP(r1, r2, index) = min from:
A: Ma(INDEX) - Mb(r1) + Mb(INDEX) - Ma(INDEX) + DP(INDEX, r2)
B: Ma(INDEX) - Mb(r2) + Mb(INDEX) - Ma(INDEX) + DP(r1, INDEX)
However, having the index in DP function is redundant. We can decrease the time complexity of our solution by removing it - index is always the next item after max(r1, r2). Thus, DP function now looks like:
DP(r1, r2) = min from:
A: Ma(max(r1, r2)+1) - Mb(r1) + Mb(max(r1, r2)+1) - Ma(max(r1, r2)+1) + DP(max(r1, r2)+1, r2)
B: Ma(max(r1, r2)+1) - Mb(r2) + Mb(max(r1, r2)+1) - Ma(max(r1, r2)+1) + DP(r1, max(r1, r2)+1)
The number of subproblems equals to M*M, because that's how many states which in the robots can be arranged. Time of computing one subproblem is constant, therefore the final complexity of this solution is O(M2).
Step 4. So is it finite algorithm? Yes, because the graph is traversed through two increasing values, r1 and r2.
Step 5. The solution is in DP(-1, -1), assuming -1 denotes that the robot wasn't used yet and the cost of moving it to Mx is 0 (because it starts at this location).
Step 4. So is it finite algorithm? Yes, because the graph is traversed through two increasing values, r1 and r2.
Step 5. The solution is in DP(-1, -1), assuming -1 denotes that the robot wasn't used yet and the cost of moving it to Mx is 0 (because it starts at this location).
The code
using System;
using System.Collections.Generic;
using System.Linq;
namespace Algos
{
public class Solver
{
private readonly int _m;
private readonly int _n;
private readonly List> _queries;
private int[][] _memo;
public Solver(int m, int n, List> queries)
{
_m = m;
_n = n;
_queries = queries;
}
public int SolveCase()
{
_memo = new int[_n + 1][];
for (int i = 0; i < _n + 1; i++)
_memo[i] = new int[_n + 1];
for (int i = _n; i >= 0; i--)
{
for (int j = _n; j >= 0; j--)
{
_memo[i][j] = -1;
}
}
return Dp(-1, -1);
}
private int Dp(int r1, int r2)
{
if (r1 + 1 == _n || r2 + 1== _n)
return 0;
if (_memo[r1 + 1][r2 + 1] != -1)
return _memo[r1 + 1][r2 + 1];
var i = Math.Max(r1, r2) + 1;
//r1 stays in place
var r2Cover = 0;
if (r2 != -1)
r2Cover = Math.Abs(_queries[r2].Item2 - _queries[i].Item1);
var d1 = Dp(r1, i);
//r2 stays in place
var r1Cover = 0;
if (r1 != -1)
r1Cover = Math.Abs(_queries[r1].Item2 - _queries[i].Item1);
var d2 = Dp(i, r2);
var queryCover = Math.Abs(_queries[i].Item1 - _queries[i].Item2);
var min = Math.Min(r2Cover + d1 + queryCover, r1Cover + d2 + queryCover);
_memo[r1 + 1][r2 + 1] = min;
return min;
}
}
class Solution
{
static void Main(string[] args)
{
//CaseSub0();
//Case0();
//Case1();
//Case2();
//RandomBigCase();
//return;
var T = int.Parse(Console.ReadLine());
for (var i = 0; i < T; i++)
{
ProcessCase();
}
}
private static void ProcessCase()
{
var @case = Console.ReadLine().Split(new[] { " " }, StringSplitOptions.RemoveEmptyEntries);
var M = int.Parse(@case[0]);
var N = int.Parse(@case[1]);
var queries = new List>(N);
for (int i = 0; i < N; i++)
{
var query = Console.ReadLine().Split(new[] { " " }, StringSplitOptions.RemoveEmptyEntries);
queries.Add(Tuple.Create(int.Parse(query[0]), int.Parse(query[1])));
}
var solution = new Solver(M, N, queries).SolveCase();
Console.WriteLine(solution);
}
private static void CaseSub0()
{
var M = 2;
var N = 1;
var queries = new List>();
queries.Add(Tuple.Create(1, 2));
var solution = new Solver(M, N, queries).SolveCase();
Console.WriteLine("Casesub0 " + solution);
}
private static void Case0()
{
var M = 5;
var N = 4;
var queries = new List>();
queries.Add(Tuple.Create(1, 5));
queries.Add(Tuple.Create(3, 2));
queries.Add(Tuple.Create(4, 1));
queries.Add(Tuple.Create(2, 4));
var solution = new Solver(M, N, queries).SolveCase();
Console.WriteLine("Case0 " + solution);
}
private static void Case1()
{
var M = 4;
var N = 2;
var queries = new List>();
queries.Add(Tuple.Create(1, 2));
queries.Add(Tuple.Create(4, 3));
var solution = new Solver(M, N, queries).SolveCase();
Console.WriteLine("Case1 " + solution);
}
private static void Case2()
{
var M = 10;
var N = 3;
var queries = new List>();
queries.Add(Tuple.Create(2, 4));
queries.Add(Tuple.Create(5, 4));
queries.Add(Tuple.Create(9, 8));
var solution = new Solver(M, N, queries).SolveCase();
Console.WriteLine("Case2 " + solution);
}
private static void RandomBigCase()
{
var M = 1000;
var N = 1000;
var queries = new List>();
var r = new Random(666);
while (queries.Count != N)
{
var from = r.Next(1, M + 1);
var to = r.Next(1, M + 1);
var t = Tuple.Create(from, to);
if (!queries.Contains(t))
queries.Add(t);
}
var solution = new Solver(M, N, queries).SolveCase();
Console.WriteLine("RandomBigCase " + solution);
}
}
}
Monday, October 31, 2016
Dynamic Programming in 5 easy steps - Examples - Set partitioning
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2016/10/dynamic-programming-in-5-easy-steps---examples---set-partitioning/
Let's continue Dynamic Programming series. Last time we have covered Text Justification problem, this time we will do something harder. The problem statement is as follows:
Given a set S of positive integers, divide it into two sets S1 and S2 such that the absolute difference between their sums is minimum.The 5 easy steps are:
If there is a set S with n elements, then if we assume S1 has m elements, S2 must have n-m elements and the value of abs(sum(S1) – sum(S2)) should be minimum.
- define subproblems, count number of subproblems
- guess (part of solution), count number of choices
- relate subproblem solutions, compute time per subproblem
- recurse + memoize OR build DP table bottom-up check subproblems acyclic/topological order, time = time per subproblem · number of subproblems
- solve original problem: = a subproblem OR by combining subproblem solutions ⇒ extra time
Taking an example, assume a set S={ 1, 6, 11, 5}.
Step 1. As previously, we want to divide the problem to subproblems.
How this can be done? Suffixes, prefixes or the mix of those two are usually the answer. It's natural to imagine that in the middle of processing the set looks at some point as follows .., 11, 5. At this very point we already assumed we are working on suffixes.
In that situation we can either include the 11 in the set S1 or in the set S2. I'll say that we take or leave the number, because we have only two choices.
Related, very important aspect - we have to track only one sum! The other one is just totalSum-chosenSetSum.
Getting back to our situation, what is the "context" of the subproblem? Does it matter how we got to this point? Not at all, what matters is only the chosenSetSum. Obviously, we have to also keep track of our current item index. Here we have it, the subproblems.
Step 2. How our guess will look like? We can increase the sum and progress with the problem,
or we can just progress with the problem, assuming we leave the item and it will be in the second set.
Step 3. Now we have to glue two pieces togeter. Our DP function will have two arguments as noted above, chosenSetSum and index.
We want to optimize for the minimum difference between the sets and that's what will be returned by the DP function. All in all, the equation is as follows:
DP(chosenSetSum, i) = min from:
- DP(chosenSetSum, i+1) //when skipping the i'th item
- DP(chosenSetSum + inputSet[i], i+1)) //when taking the i'th item
The corner case is DP(X, inputSet.Length) = totalSum-X, because that's the end of partitioning.
The time complexity of this approach is:
time = time per subproblem · number of subproblems, so time = O(1) * O(sum * n) = O(sum * n)
Yey, we have pseudo-polynomial time solution.
Step 4. Is it actually an acyclic graph of DP function invocations? My reasoning here is that we have two dimensions (chosenSetSum and item index) where both increase and there is an end when the second variable reaches input set cardinality, thus it's finite algorithm.
Step 5. We start with chosenSetSum=0 and at the first index, therefore our solution is at DP(0,0).
Step 4. Is it actually an acyclic graph of DP function invocations? My reasoning here is that we have two dimensions (chosenSetSum and item index) where both increase and there is an end when the second variable reaches input set cardinality, thus it's finite algorithm.
Step 5. We start with chosenSetSum=0 and at the first index, therefore our solution is at DP(0,0).
The Code
Having the 5 steps figured out, it's relatively easy to code the solution.
Pure DP algorithm coded without memorization
private class Partitioner
{
private readonly int[] _inputSet;
private readonly int _inputSetSum;
public Partitioner(int[] inputSet)
{
_inputSet = inputSet;
_inputSetSum = _inputSet.Sum();
}
public void Solve()
{
DP(0, 0);
}
private int DP(int chosenSetSum, int i)
{
if (i == _inputSet.Length)
//Note: returning the difference between chosenSetSum and skippedSetSum,
//not the skippedSetSum (which would be _inputSetSum - chosenSetSum)
return Math.Abs(_inputSetSum - 2 * chosenSetSum);
var chooseCurrentNumberScore = DP(chosenSetSum + _inputSet[i], i + 1);
var skipCurrentNumberScore = DP(chosenSetSum, i + 1);
var minDiff = Math.Min(skipCurrentNumberScore, chooseCurrentNumberScore) ;
return minDiff;
}
}
How cool is that? 6 lines of code for almost working solution!Memoization added
private class Partitioner
{
private const int Marker = -1;
private readonly int[] _inputSet;
private readonly int _inputSetSum;
private readonly int[][] _memo;
public Partitioner(int[] inputSet)
{
_inputSet = inputSet;
_inputSetSum = _inputSet.Sum();
_memo = new int[_inputSetSum][];
for (var i = 0; i < _inputSetSum; i++)
{
_memo[i] = new int[_inputSet.Length];
for (var j = 0; j < _inputSet.Length; j++)
_memo[i][j] = Marker;
}
}
public void Solve()
{
DP(0, 0);
}
private int DP(int chosenSetSum, int i)
{
if (i == _inputSet.Length)
//Note: returning the difference between chosenSetSum and skippedSetSum,
//not the skippedSetSum (which would be _inputSetSum - chosenSetSum)
return Math.Abs(_inputSetSum - 2 * chosenSetSum);
if (_memo[chosenSetSum][i] != Marker)
return _memo[chosenSetSum][i];
var chooseCurrentNumberScore = DP(chosenSetSum + _inputSet[i], i + 1);
var skipCurrentNumberScore = DP(chosenSetSum, i + 1);
var minDiff = Math.Min(skipCurrentNumberScore, chooseCurrentNumberScore);
_memo[chosenSetSum][i] = minDiff;
return minDiff;
}
}
Full solution with parent pointers and examples
using System;
using System.Collections.Generic;
using System.Linq;
public class DP_SetPartition
{
static void Main(String[] args)
{
PrintSolution(new int[0]);
PrintSolution(new[] { 3 });
PrintSolution(new[] { 3, 3 });
PrintSolution(new[] { 3, 2 });
PrintSolution(new[] { 1, 4, 2 });
PrintSolution(new[] { 1, 2, 4 });
PrintSolution(new[] { 1, 1, 5, 1, 1, 1 });
PrintSolution(new[] { 1, 6, 11, 5 });
PrintSolution(new[] { 1, 6, 11, 5 });
PrintSolution(new[] { 25, 21, 20, 17, 8 });
PrintSolution(new[] { 1, 5, 6, 10 });
PrintSolution(new[] { 3, 1, 4, 2, 2, 1 });
PrintSolution(new[] { 200, 200, 300, 300, 400, 400, 1000, 1000 });
PrintSolution(new[] { 100, 100, 200, 200, 300, 300, 400, 400, 1000, 1000 });
Console.ReadLine();
}
private static void PrintSolution(int[] set)
{
Console.WriteLine($"Set: {string.Join(", ", set)}");
int[] set1;
int[] set2;
new Partitioner(set).Solve(out set1, out set2);
Console.WriteLine($"A: {string.Join(", ", set1)} \t\t B: {string.Join(", ", set2)}, sumdiff: {Math.Abs(set1.Sum() - set2.Sum())}");
Console.WriteLine();
}
private class Partitioner
{
private const int Marker = -1;
private readonly int[] _inputSet;
private readonly bool[][] _parentPointers;
private readonly int _inputSetSum;
private readonly int[][] _memo;
public Partitioner(int[] inputSet)
{
_inputSet = inputSet;
_inputSetSum = _inputSet.Sum();
_memo = new int[_inputSetSum][];
_parentPointers = new bool[_inputSetSum][];
for (var i = 0; i < _inputSetSum; i++)
{
_memo[i] = new int[_inputSet.Length];
_parentPointers[i] = new bool[_inputSet.Length];
for (var j = 0; j < _inputSet.Length; j++)
{
_memo[i][j] = Marker;
}
}
}
public void Solve(out int[] set1, out int[] set2)
{
DP(0, 0);
var chosenSet = new List<int>();
var skippedSet = new List<int>();
var sum = 0;
var i = 0;
while (i != _inputSet.Length)
{
var choose = _parentPointers[sum][i];
if (choose)
{
chosenSet.Add(_inputSet[i]);
sum += _inputSet[i];
}
else
{
skippedSet.Add(_inputSet[i]);
}
i++;
}
set1 = chosenSet.ToArray();
set2 = skippedSet.ToArray();
}
private int DP(int chosenSetSum, int i)
{
if (i == _inputSet.Length)
return Math.Abs(_inputSetSum - 2 * chosenSetSum);
if (_memo[chosenSetSum][i] != Marker)
return _memo[chosenSetSum][i];
var chooseCurrentNumberScore = DP(chosenSetSum + _inputSet[i], i + 1);
var skipCurrentNumberScore = DP(chosenSetSum, i + 1);
var minDiff = skipCurrentNumberScore;
if (chooseCurrentNumberScore < skipCurrentNumberScore)
{
minDiff = chooseCurrentNumberScore;
_parentPointers[chosenSetSum][i] = true;
}
_memo[chosenSetSum][i] = minDiff;
return minDiff;
}
}
}
It's working!
Tuesday, October 25, 2016
Dynamic Programming in 5 easy steps - Examples - Text Justification
Please find the updated version of this post here: https://piotr.westfalewicz.com/blog/2016/10/dynamic-programming-in-5-easy-steps---examples---text-justification/
Lately I spent a relatively great amount of time revising Algorithms and Data Structures. It's a broad subject, but for me personally I found the Dynamic Programming as the abandoned and unused method. It's also considered as one of the hardest methods to master, with few examples on the internet. Let's contribute a little with this post series. Today I will cover the first problem - text justification. The problem is from MIT lectures and I highly recommend well explained videos along with notes from course 6.006: Introduction to algorithms - fall 2011.
Text justification
Given a text, split it into multiple lines so it is “nicely” distributed between each line.What does it mean? Take a look at the example:
We can clearly see that eager approach won't produce good results in all cases.
Mathematically, given a badness(i, j) function for line of words[i : j], we seek for such a splitting that the sum of all badness is minimum.
Let's assume the badness function is predefined as follows:
∞ if total length > page width, else (page width − total length)3So in the example above, the bad splitting would have:
- page width = 16
- first line length = 4+4+4+2 = 16, badness of the first line = 0
- second line length = 4, badness = (16-4)3=1728
- third line length = 16, badness = 0
- badness sum = 1728
The good splitting would have:
- first line length = 4+4+1 = 9, badness of the first line = (16-9)3=343
- second line length = 9, badness = (16-9)3=343
- third line length = 16, badness = 8
- badness sum = 694
The second splitting has smaller total badness sum, thus it's a better splitting.
Dynamic Programming in 5 easy steps
On the MIT course, there is presented an approach to DP in 5 easy steps. Those are:
- define subproblems, count number of subproblems
- guess (part of solution), count number of choices
- relate subproblem solutions, compute time per subproblem
- recurse + memoize OR build DP table bottom-up check subproblems acyclic/topological order, time = time per subproblem · number of subproblems
- solve original problem: = a subproblem OR by combining subproblem solutions ⇒ extra time
Well, the steps don't have to be executed always in order. Let's try to figure out the second step. We know where our line begins, it's on ith position. Where is the end of the line? We don't know. So let's check all possibilities, that's from ith onward and take the smallest badness. So now we know what's our subproblems in first step are - suffixes of word[i:]. That's pretty much the algorithm. The third step will look like:
DP(i)=for j in i+1...n+1 take min from (DP(j) + badness(i, j))The great thing is about DP that DP(j) considered to be free (because we compute the subproblem once and memorize the answer). Therefore the total time needed by this algorithm is:
time = time per subproblem · number of subproblems, so time = O(n) · O(n) time = O(n^2)The fourth point is about proving that this really works and the time needed is finite. We compute the answer from the end of the words, down to word number 0. The recursive DP function always accesses greater indexes, therefore time needed is finite. Lastly, we have to find our answer. Here, obviously it's DP[0]. Easy? Yup, let's code it!
The code
using System;
using System.Collections.Generic;
using System.Linq;
namespace Algos
{
public class DP_TextJustification
{
static void Main(String[] args)
{
//please note: this is not a production-ready solution!
PrintSolution(" ", 10);
PrintSolution("oneword", 10);
PrintSolution("one line", 10);
PrintSolution("two lines", 6);
PrintSolution("blah blah blah blah reallylongword", 14);
PrintSolution("blah blah blah blah reallylongword 1", 14);
var txt1 = "Lorem ipsum dolor sit amet, consectetur adipiscing elit. " +
"Praesent varius urna eget lacinia pharetra. " +
"Vivamus lacinia in dui vitae sodales. " +
"Aliquam auctor justo nec condimentum pretium. " +
"Curabitur egestas tellus dolor, vel tempus lacus blandit vitae. " +
"Cras dapibus scelerisque ex nec gravida.";
PrintSolution(txt1, 60);
PrintSolution(txt1, 70);
PrintSolution(txt1, 80);
PrintSolution(txt1, 90);
PrintSolution(txt1, 100);
Console.ReadLine();
}
public static void PrintSolution(string txt, int width)
{
Console.WriteLine($"Test length: {txt.Length}, line width: {width}");
foreach (var line in new Justifier(txt, width).Solve())
{
Console.WriteLine("{0,-" + width + "}|", line);
}
Console.WriteLine();
}
private class Justifier
{
private const int Marker = -1;
private readonly int _width;
private readonly string[] _words;
private readonly int[] _parentPointers;
private readonly int[] _memo;
public Justifier(string text, int width)
{
_width = width;
_words = text.Split(new[] {" "}, StringSplitOptions.RemoveEmptyEntries);
_parentPointers = new int[_words.Length];
_memo = new int[_words.Length];
for (var i = 0; i < _memo.Length; i++)
{
_memo[i] = Marker;
}
}
public List<string> Solve()
{
DP(0);
var result = new List<string>();
var from = 0;
while (from != _words.Length)
{
var next = _parentPointers[from];
result.Add(string.Join(" ", _words.Skip(from).Take(next - from)));
from = next;
}
return result;
}
private int DP(int i)
{
if (i == _words.Length) //no words in line is the end of justification
return 0;
if (_memo[i] != Marker) //if we have solution calculated, return it
return _memo[i];
var minBadness = int.MaxValue;
for (var j = i + 1; j <= _words.Length; j++)
{
var badness = Badness(i, j) + DP(j);
if (minBadness > badness)
{
_parentPointers[i] = j; //remember best choice
minBadness = badness;
}
}
_memo[i] = minBadness; //remember solution
return minBadness;
}
private int Badness(int i, int j)
{
var lengthOfWords = _words.Skip(i).Take(j - i).Sum(s => s.Length);
var numberOfSpaces = j - i - 1;
if (lengthOfWords + numberOfSpaces > _width)
return 10*1000*1000;
return (int)Math.Pow(_width - lengthOfWords - numberOfSpaces, 3);
}
}
}
}
To the solution in 5 easy steps I've added parent pointers - a simple way to remember the best solution from DP. The result is as follows:If we don't care about justifying the last line, we can easily modify the badness function to return no cost for the last line:
private int Badness(int i, int j)
{
var lengthOfWords = _words.Skip(i).Take(j - i).Sum(s => s.Length);
var numberOfSpaces = j - i - 1;
if (lengthOfWords + numberOfSpaces > _width)
return 10*1000*1000;
if (j == _words.Length) //don't care about last line
return 0;
return (int)Math.Pow(_width - lengthOfWords - numberOfSpaces, 3);
}
In this case, the result will be much different in some cases:
Subscribe to:
Posts (Atom)








